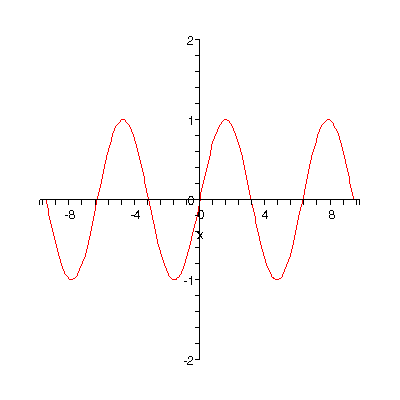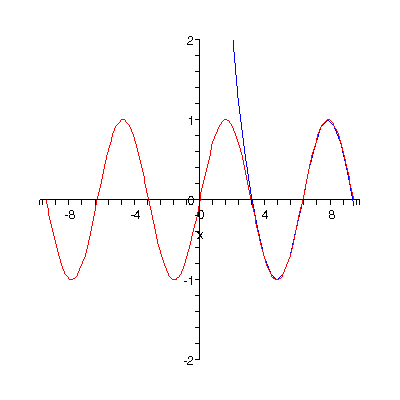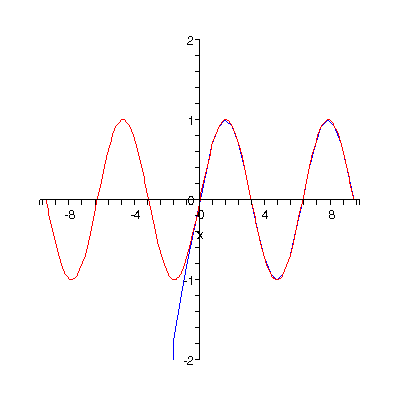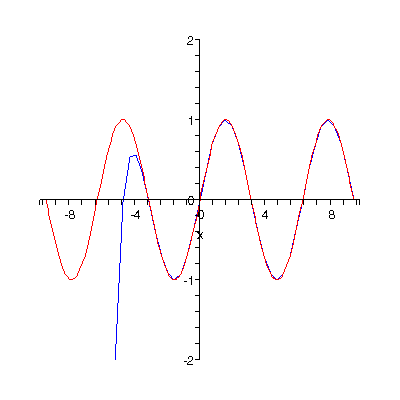
Las integrales son el area debajo de una curva delimitada por 2 puntos sobre el eje de las x, un punto inicial o punto a y un punto final o punto b.
Al derivar una funcion y evaluarla entre esos 2 puntos se obtiene el area que esta debajo de la curva, como lo muestra la imagen, se puede conocer el area sombreada que se muestra integrando la funcion y evaluandola entre los 2 puntos.

(Se supone que la base inferior de todos los trapecios mide lo mismo)
y lo que se hace es sacar el area de cada uno de los trapecios y luego sumarlas todas para obtener mas o menos el area sombreada.
Mientras mas trapecios se coloquen mas precisa sera la aproximacion, y tambien mientras mas trapecios se coloquen su base inferior tiende a ser 0.

El area de un trapecio se obtiene como muestra la imagen de arriba, asi que solo hay que hacer un pequeño analisis matematico para obtener una ecuacion que nos permita obtener el area de los trapecios en la curva:

Se separa al trapecio como si estuviera compuesto de un triangulo y un rectangulo.
La serie de ecuaciones que se muestran abajo son un desarrollo en el cual se trata al trapecio priero sacando el area del rectangulo y luego la del triangulo y sumandolas. Luego se simplifican las ecuaciones y se obtiene la que estamos buscando.

El area del rectangulo es bxh y la base es la resta entre los puntos x1-x0 la altura es el punto y1.
El area del triangulo es (bxh)/2
la base es la misma que la del rectangulo y la altura es la resta del punto y0-y1.
Se factorizan y simplifican las ecuaciones.
Por ultimo queda la ecuacion del area de cada trapecio.

Pero no todas las funciones son faciles de integrar, de hecho algunas ni siquiera se pueden integrar, asi que se usan otros metodos que se aproximan a una integral.
REGLA DEL TRAPECIO
Es la primera de las fórmulas de integración cerrada de Newton–Cotes. Corresponde al caso donde el polinomio en la ecuación de integración es de primer orden:

Geométricamente, es equivalente a aproximar el área del trapezoide bajo la línea recta que conecta f(a) y f(b).
La integral se representa como:
I ≈ ancho x altura promedio

Error de la regla trapezoidal:
Una estimación para el error de truncamiento local de una sola aplicación de la regla trapezoidal es:

El metodo del trapecio es uno de los mas antiguos y sirvio de base para desarrollar las integrales(junto con otros metodos parecidos como el de los rectangulos), pero nunca seran exactos, solo se aproximan.
Este metodo consiste en "llenar" el area que se quiere conocer con trapecios como lo muestra la imagen:
http://www.scribd.com/doc/4755474/mat31